차동증폭기


- V2와 V1전압을 똑같이 맞추기 위해 R1와 R2를 V2에 달아준다.
- 중첩의 원리 : V2가 나올때 V1이 없다고 가정. V2가 비반전 입력단자로 들어갈때 op-amp 저항이 무한대. R1과 R2에 의해 나눠진다 (R2/(R1+R2))*V2. 비반전 증폭기처럼 보인다. (1+R2/R1)을 곱해주면 (R2/R1)*V2
- V1이 나올때 V2가 없다고 가정. 입력이 v1인 반전 증폭기처럼 보인다. -(R2/R1)*V2
- (R2/R1)*V2+ -(R2/R1)*V1 = R2/R1(V2-V1)

- 두 저항이 같으면 빼기 (differential)

- 이 특성을 이용하면 양쪽 단의 전압 차이를 읽어낼 수 있다.
- Sensing 저항 1ohm 일때 R2 : R1의 비가 100이면 전류가 흐를때 1V가 뜸. 10mA의 전류가 sensing저항에 흐르는 것을 알 수있다.
- Current monitoring IC회로

차동증폭기



- 나가는 전류와 들어오는 전류가 같은 전류이다. 차동 증폭기의 입력저항이 2kOhm.
- 단점: 입력저항을 크게 만들기가 어렵다.
계측 증폭기
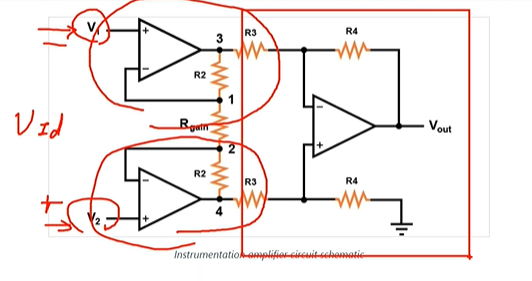
- Op-amp 3개를 써서 만든 차동증폭기. 입력저항이 작은것을 해결.
- 비반전증폭기 입력단자가 입력쪽에서 보이는 형태 : 입력저항 무한대.
- 뒷단이 차동증폭기. 두번 증폭을 해서 증폭도도 크다.
- 하나의 IC 칩으로 나온다.
반전 증폭기를 이용한 덧셈기 회로

- V2를 ground 시켜 죽임. Virtual short개념에 의해서 R1옆도 ground 시킴. R2 → gnd사이 저항. 없는것과 마찬가지 이득이 -Rf/R2(V1)
- V1을 gnd 시킴. R1 →gnd 사이 저항. 없는것과 마찬가지. 이득이 -Rf/R2(V2)
- 최종 출력 V_o = -Rf/R2(V1) + -Rf/R2(V2) = -R_f[V1/R1+V2/R2+V3/R3+...]
- 덧셈기 회로 (가중치 → weighted summer)
- 연산 증폭기 (Operational Amplifier → op amp): 다양한 연산을 할 수 있음.
Op-amp의 장점: Op-amp를 바꿔도 V_o의 값이 같다. 저항의 비에 따라 증폭도가 결정되기 때문에.

074와 741의 주파수를 비교했을 때

074 의 동작주파수가 741 보다 크다.
- 0dB을 지나갈때의 주파수: 모든 그래프들이 공통으로 지나가는곳 이득이 1
- Unity Gain Frequency, Unity Gain Bandwidth 단위이득 주파수가 클수록 고속동작 가능
Slew Rate


- Op-amp의 출력이 빨리 따라가지 못하는 상황
- 741 op-amp의 slew rate 0.5V/us
Op-amp의 고유 성능 지표 Slew rate


- TL 074 model의 slew rate: 8.5V/1us. 훨씬 더 고속에서 동작 하기에 적합한 op-amp
Op-amp 를 사용할 때 마주칠 문제

- 하나의 supply 전압만 가지고도 증폭기로 사용할 수 있게 변환해주어야 한다.
반전증폭기
- 지금까지는 +/- 12V를 사용했다. 이렇게 dual supply로 구동시키면 두 입력단자의 bias DC전압과 출력의 bias DC전압이 +/- 12V의 한가운데인 0V가 되어야함.
- Sin 파형이 0V기준으로 들어온다고 가정했기 때문에 direct로 연결 가능
- DC level이 달라지면 capacitor를 달아준다.

- Input offset 전압 19.25uV, bias 전류가 증폭된 910.3uV
- Offset이 없다고 치면 입력단자의 출력단자의 전압이 0V.
Dual supply가 아닌 single supply로 바꾸면 어떻게 될것인가?
- V_cc 전압은 그대로 간다,
- -12V를 위로 쭉 밀어줘서 0V로 바꿔줘야함
- 원래 0V인 한가운데 전압이 V_cc/2 가 됨.

입력신호와 RL의 gnd가 아닌 내가 설계하는 증폭기



- 6V를 걸게되면 virtual short에 의해서 외부에서 입력되는 전압은 0V인데 op-amp의 bias전류는 6Vdc.
- Coupling capacitor를 달아서 6V를 기준으로 하는 sin파형으로 바꿔준다.

- 전압원 2개쓰기 싫어서 회로를 바꿔줬는데 6V 전압원을 또 만든다?
- 실제로 구현할때는 저항으로 분배해준다.



- 신호 입장에서 dual supply 일때 gnd였음. Bias 입장에서도 gnd, 신호 입장에서도 gnd.
- DC 입장에서는 V_cc/2. 신호입장에서는 1kohm 병렬 1kohm 으로 보인다. 완벽하게 single supply에서도 여기가 gnd로 보이게 하고싶으면 capacitor를 단다. 높은 주파수 : capacitor가 gnd로 보인다.

- 2kohm 저항에 12V → 6mA
- 6mA * 12V = 72mW의 파워소모가 생기고있다.
- 저항을 10k 10k 쓰면 0.6mA → 흐르는 전류가 1/10로 줄어듦. →7.2mW의 파워소모 (작아짐)
- 큰 저항값을 적용하면 파워소모를 줄일 수 있다. 10kohm ~ 100kohm 사이.
최종 반전 증폭기

Single Supply 비반전 증폭기



- capacitor 때문에 bias전류가 안흐른다. DC전류가 흐를 수 있는 길이 끊김. 다른쪽으로 별도의 길을 만들어줘야한다.

- Pull-up 저항을 만들어줘서 DC전류가 흐를 수 있는 길을 터준다.

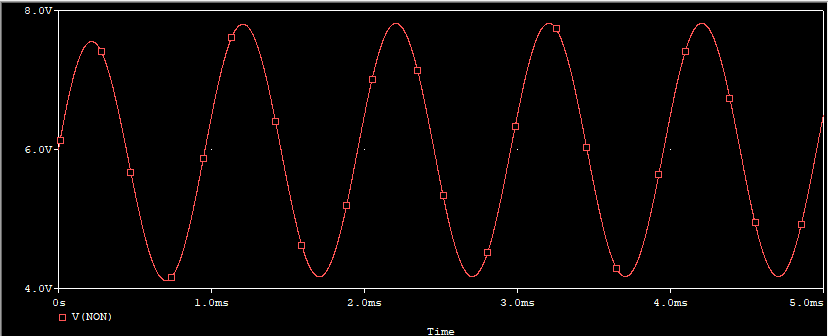


- Pull-up 저항의 값을 10kohm // 10kohm
- 입력 bias를 없애면서 pull-up 저항의 역할을 할 수 있음


DC를 걷어내고 순수한 신호만 가져오고싶다: coupling capacitor를 부하에 연결


- 두개의 CR구조 : high pass filter 형태


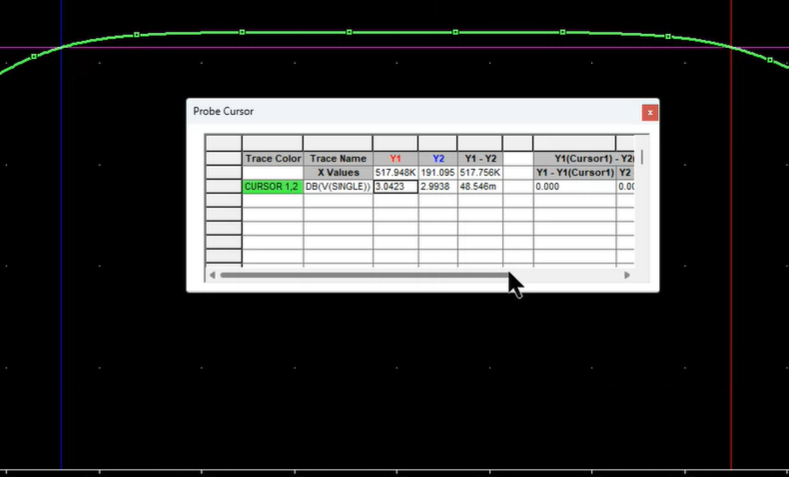
- 가운데: single supply 비반전을 구동 시킬 수 있는 구간, 중간 주파수 대역
- 대역폭: 3Hz~ 518 kHz

- Coupling capacitor가 저주파 영역을 만듦. 왼쪽
- 내가 달아주는 C값이 저주파 영역의 bandwidth를 결정한다.
- C값이 커지면 cut-off frequency가 작아짐.
- Coupling capacitor를 일반적으로 크게 만든다 → 대역폭을 넓힌다.
차동증폭기

- 공통신호를 입력에 넣으면 출력에 0이 나온다

- 입력저항을 크게 만들기 위해서 차동증폭기를 앞단에 달아준다. 앞쪽에서 증폭을 하고 뒤쪽에서 증폭을 또 한다.
\

- Bounded input → bounded output : 안정된 시스템
- Impulse 입력을 넣었을때 출력은 수렴하는 신호가 되면 안정된 시스템이다.
- Step response를 보기위해 펄스신호를 집어넣는다.

- 하나의 전원으로 op-amp를 작동시켜야함.

- 단순한 전원분배를 통해서 6V 전압을 만든다.
- Capacitor의 역할: DC 6V를 깨끗하게 보기위함 → noise 빠지게 하기위함.


Op-amp 보강: comparator

- Op-amp와 comparator의 내부구조는 거의 비슷하다. Op-amp에 feedback을 걸지 않으면 comparator와 같다.
- Op-amp: feedback을 걸어서 증폭하기 위한 목적. 선형적인 특성이 있다. 입력이 들어갔을 때 출력이 선형적으로 변함.

- +쪽 이 -쪽보다 크면 1 작으면 0.
- 선형적 구조보다 회로 블럭이 더 간단하다. → 가격이 싸다.

- 출력이 엄청 빨라질 수 있다. Slew rate가 크다. → 고속동작이 가능하다.

- 출력이 논리 0, 1 이 나오는 것 처럼 동작.
- V1 > V2 → V_o에 아무것도 출력이 안된다. Open collector이기 때문. 뒷단에 IC를 달아주어 출력전압을 출력해줘야함.

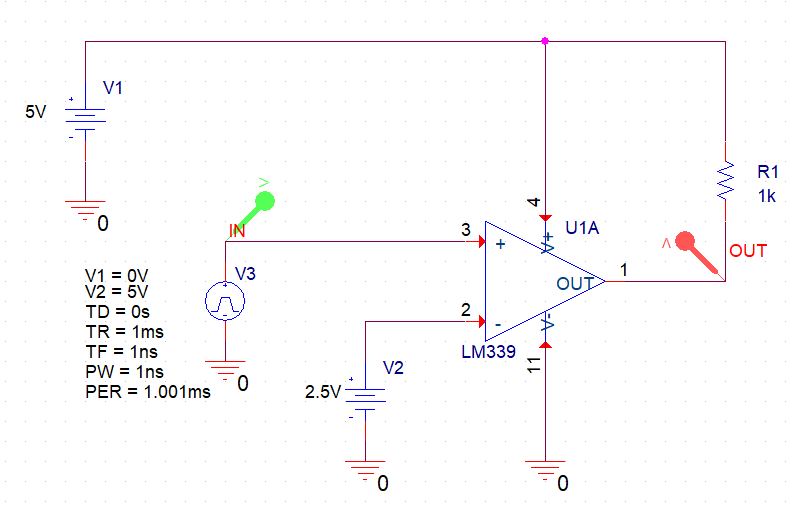
- 출력과 전압원에 pull-up 저항 R1 연결
비교대상 V2가 2.5V일때

비교 대상 V2가 1V일때

비교대상에 따라 펄스의 폭이 늘렸다 좁혔다 할 수 있음. → PWM 신호를 생성할 수 있음.
조금더 직관적으로 이해가 되게 회로를 수정하면 입력을 -에, 출력을 +에 연결

1V일때 20% duty cycle

2.5V일때 50% duty cycle

4V일때 80% duty cycle

'회로 공부' 카테고리의 다른 글
| 전원회로 (1) | 2024.11.11 |
|---|---|
| OP-Amp(2) (0) | 2024.11.11 |
| OP-Amp (0) | 2024.11.11 |
| Switching 응용회로 / Comparator (1) | 2024.11.11 |
| MOSFET Load Switching 회로 (0) | 2024.11.11 |